- El Pensadero de Canek - https://aztlan.fciencias.unam.mx/pensadero -

¿A la fregada?

Posted By Canek On marzo 29, 2006 @ 1:29 PM In Academia | 2 Comments

En Lógica Matemática con Francisco Hernández Quiroz nos dio Göedel para niños (©).

Sea 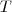una teoría matemática (un subconjunto del cálculo de predicados con una interpretación 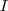y un universo U), con 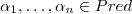$\alpha_{1},\ldots,\alpha_{n}\in{}Pred$ como axiomas. Entonces

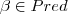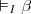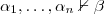Existe $\beta\in{}Pred$ tal que $\vDash_{I}\beta$ pero $\alpha_{1},\ldots,\alpha_{n}\nvdash\beta$ (para todo sistema de demostración 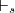$\vdash_{s}$ como los vistos en clase). En pocas palabras, existen fórmulas 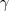$\gamma$ tales que 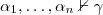$\alpha_{1},\ldots,\alpha_{n}\nvdash\gamma$ y $\alpha_{1},\ldots,\alpha_{n}\nvdash\lnot\gamma$ .
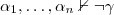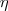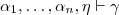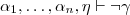Si agregamos un axioma adicional $\eta$ tal que $\alpha_{1},\ldots,\alpha_{n},\eta\vdash\gamma$ o $\alpha_{1},\ldots,\alpha_{n},\eta\vdash\lnot\gamma$ , entonces 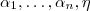$\alpha_{1},\ldots,\alpha_{n},\eta$ con $\vdash$ son inconsistentes.

(Antes de que mis amigos matemáticos me salten encima para decir que cualquier cosa de arriba esté mal: tengan en cuenta de que es la versión para niños).

Después de decirnos eso, se dio el siguiente diálogo:

Francisco: Y bueno, después de que Göedel demostró esto, mandó a la lógica a…
Yo: ¿A la fregada?

^[1] Imprimir entrada ^[1]

2 Comments (Open | Close)

2 Comments To "¿A la fregada?"

#1 Comment By Omar Antolín On marzo 29, 2006 @ 6:11 PM

Leí tu advertencia, pero aún así dejo un comentario, nomás para probar el plugin de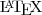 $\LaTeX$ …

Lo más importante que te faltó es decir a qué sistemas se le aplica el teorema. Algunos sistemas axiomáticos sí son completos, el chiste del teorema de Gödel es que los interesantes no lo son. La hipótesis precisa es latosa de formular, pero escencialmente el teorema se aplica a cualquier sistema suficientemente rico como para expresar la aritmética de Peano.

En el segundo punto que pones hay algo mal. En la teoría de conjuntos con los axiomas de Zermelo-Fraenkel, el axioma de elección no puede ser probado ni refutado, pero ni agregarlo, ni agregar su negación produce un sistema inconsistente (si suponemos que ZF era consistente para empezar).

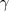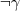Ese es un ejemplo famoso, pero intuitivamente es claro que si no se puede probar $\gamma$ o $\lnot\gamma$ , podría que simplemente no hay información para concluir algo acerca de 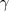$\gamma$ y que podríamos agregar axiomas que decidan la cuestión.

Supón que el único axioma que hay es “Toda rata es gris o blanca”. En ese sistema no podemos demostrar que todas las ratas son blancas ni que no todas lo son. Obviamente tanto agregar el axioma “Todas las ratas son blancas”, como agregar el axioma “Existe una rata gris” da un sistema consistente.

Finalmente, un error de dedo: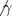 $\not\gamma$ debía ser $\lnot\gamma$ .

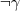#2 Comment By Canek On marzo 29, 2006 @ 10:16 PM

Ok ok ok… y gracias por la corrección… pero lo importante es que sí se va a la fregada, ¿no?